在人教版高中物理必修一教材第二章《匀变速直线运动的研究》中，有关匀变速直线运动速度、时间、位移三者关系有很重要的几个推论，其中较为重要的是有关平均速度与瞬时速度关系的推论，连续相等时间内的位移之差的推论和初速度为0的匀变速直线运动的时间以及位移的几个推论，其次是有关位移中点速度的推论。
　　这几个推论如果能熟练运用，在解决匀变速直线运动题目时，往往让复杂的题目简单化，甚至一眼就能看出答案来。但是学生掌握起来却有些难度，就是老师引导他们细心推导出来，在面对具体题目的时候，学生却不会用这个知识去解决问题，往往习惯于从基本的关系出发，经过繁复的运算和推导来求解，既浪费时间，又增加了出错的概率，得不偿失。
　　那么，如何讲好这几个推论呢？我觉得只要教师牢牢抓住物理知识中的对称美，让学生在感受物理学知识的美中去学习和掌握知识，那么，这些需要死记硬背的结论就会变成学生自己的东西，用起来也会得心应手的。学生从学习中感受到了美的震撼，对知识就有了一定的审美体验，而这也恰恰是培养学科素养要求的东西。
　　其实这些推论，我大致把它分为三类。
　　第一类是关于“时间中点”和“位移中点”的。即匀变速直线运动的平均速度等于中间时刻的瞬时速度，即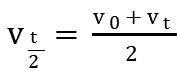 。另一个是匀变速直线运动在某段位移中点的速度等于初速度的平方加末速度的平方除以2再开平方，即 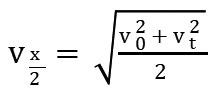。这两个问题其实就具有对称性，让学生体会到问题的对称性，也就让学生牢牢记住了问题的研究本身，那么结论就是自然的，对结论理解上去了，运用也就很自然了。
　　第二类是有关初速度为0的匀变速直线运动的两个推论。我总结为“相等时间位移之比”和“相等位移时间之比”，学生很容易感受到这两个问题的对称性和互补性。在研究中必然充满了浓厚的兴趣。他们很快就自己得到了初速度为0的匀变速直线运动在连续相等的时间内的位移之比为1∶3∶5∶7……，也通过对对称性的体验，很快得到初速度为0的匀变速直线运动在连续相等的位移上所用时间之比为
　　1∶ 2-1∶3- 2∶4- 3……这一结论。
　　这两个对称性结论再加上匀变速直线运动在连续相等时间内的位移之差是个常数等于at2。学生很容易记住，教师给出匀变速直线运动推论的2+1+2（“2”匀变速直线运动时间中点的速度和位移中点的速度推论；“1”连续相等时间内的位移之差是个常数；“2”初速度为0的匀变速直线运动在连续相等时间内的位移之比和通过连续相等位移所用时间之比。）这一形象说法，总的看来，整体知识也具有对称性了。
　　写到这里，我又禁不住想起德布罗意对物质波的研究，正是基于人们研究光的波动性的时候忽略了光的粒子性这一事实为启发，得到人们研究实物粒子的时候过多关注了实物的粒子性而忽略了实物粒子的波动性这一对称性问题，从而提出了物质波理论。这正是对学科中的对称美的极度体验得到的结果。
　　可见在教学中，如何让学生体验到学科的对称美是教学中的重要任务，也是学科素养养成的关键点。