崔伟红
　　几何证明问题是培养学生数学核心素养的重要手段，是初中数学考查学生逻辑推理能力、空间思维能力、分析问题和解决问题能力的常规题型。对于此类题目，学生常会出现诸如有思路但不会写过程、思维不严密、逻辑关系错误、想当然添加条件等多种问题。究其原因，主要有以下几方面：一是学生对所学定理未能深入理解，二是学生推理能力不足，三是学生缺乏证明题的解题方法。下面将自己一些几何证明题的教学体会总结如下：
　   一、注重已有的事实和确定的规则，数形结合深入理解
　　已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则等）是证明题的基础，若已有的事实和确定的规则理解不了，不知道其条件与结论、不清楚其用途，学生自然就不明白如何用它来证明。因此注重已有事实和确定规则探索、归纳、证明过程，让学生清楚定理的整个形成过程就尤为重要。让学生在探索过程中了解数学研究问题的一般方法，在证明过程中理解数学思维的严密性，形成逻辑推理和演绎推理的能力。渗透数形结合思想，使学生将图形语言、符号语言、文字语言三种语言相融合，让学生从不同角度深入理解已有的事实和确定的规则。
　　 二、注重难度递进的练习，循序渐进建立信心
　　数学学习离不开练习，知识的掌握、能力的形成、自信心的建立更离不开练习巩固。学完定理之后，教师可以先给学生训练一些推理性的填空题，让学生清楚用它证明的一般格式和规范，再训练一些一两步的推理证明题目。从此处入手，可以使学生在证明过程进一步理解相关知识，明确其用途、用法，从而树立学习几何证明问题信心，使学生消除恐惧心理，不断培养学习兴趣。
　　 三、注重解题方法归纳，让学生有章可循
　　“数学是研究数量关系和空间形式的科学”，将这些规律总结归纳出来便于进一步解决其他问题。因此，老师要从证明题解题中总结方法，让学生便于操作，易于接受。证明题解题“六部曲”：一读二标三联想，四析五写六检查，会大大帮助学生规范地解答证明题。
　　一读，对照图形读题目条件及结论，画出诸如线段、角之间的等量关系和不等关系、点的位置、图形的形状等；
　　二标，根据条件将图形中的条件，如题目中图形线段长度、角度、线段关系、角的关系等能标注的标在题目中的图形上，以便直观地找出题目条件，为形成证明思路做好准备；
　　三联想，是根据条件联想相关的定理，利用该条件一步或两步推出一些线段、角的关系、图形的形状，可能需要的辅助线等；
　　四析，从问题入手推出使问题成立所需要的条件，一步步推到题目已知条件；若不能推到已知条件，再从已知的条件开始向问题方向推，直到思路打通。最后归纳推理证明过程分为几部分，按照前后顺序整理思路。如：
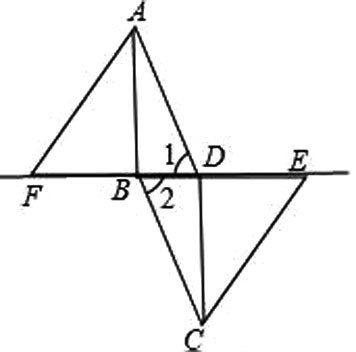
　　如图，在平行四边形ABCD中，连接BD，在BD的延长线上取一点E，在DB的延长线上取一点F，使BF=DE，连接AF、CE.
　　求证：AF∥CE.
　　引导学生分析：要证AF∥CE需要依据平行线的判定定理证明∠AFE=∠CEF，要证∠AFE=∠CEF需证△AFD和△CEB全等，而要证△AFD和△CEB全等需要找三角形全等的三组条件。此时，需要从已知条件“BF=DE和平行四边形ABCD”来推理寻找条件。而由“BF=DE和平行四边形ABCD”我们很容易就可以证得FD=EB，∠1=∠2，AD=CB，问题思路随之打通。第一步由“BF=DE”证FD=EB，第二步由“平行四边形ABCD”证∠1=∠2，AD=CB，第三步证△AFD和△CEB全等，最后一步证AF∥CE。
　　五写，按照分析出的思路，将其转化为符号语言，一步一步书写出来；
　　六检查，检查证明过程有无思维跳跃？有无逻辑关系的错误？有无想当然的添加条件？有无笔下失误写错字母？是否规范？如果有就及时改正。
　　当然几何证明题要做好，不是一个简单的过程，它是一个长期系统的工作。其中学生理解相关定理是基础，教会学生分析几何问题的方法是关键，养成学生严密的思维能力是核心，只有我们扎扎实实地做好每一个环节，学生的数学核心素养就会不断提升，几何证明题解题能力也就能不断提高。
　　（作者单位：陕西省旬邑县实验中学）